Ascent Formula is an expression which gives the value of height upto which a liquid rises upward or falls downward in a capillary tube.
Derivation of Ascent Formula
Consider a capillary tube of radius $r$ open at both ends is dipped into a liquid which wets the walls of the tube such as water. For such a liquid, the angle of contact will be acute and hence the meniscus will be concave.
The surface of the liquid is in contact with the walls of the tube all along the circle of circumference $2πr$, where $r$ is the radius of the tube. Then, surface tension $(T)$ of the liquid acts inward along the tangent of the meniscus. So, the liquid pulls the tube inward all along the circle with the force per unit length $(T)$.
According to Newton’s third law of motion, the tube also gives an equal and opposite reaction $(R)$ to the meniscus of the liquid.
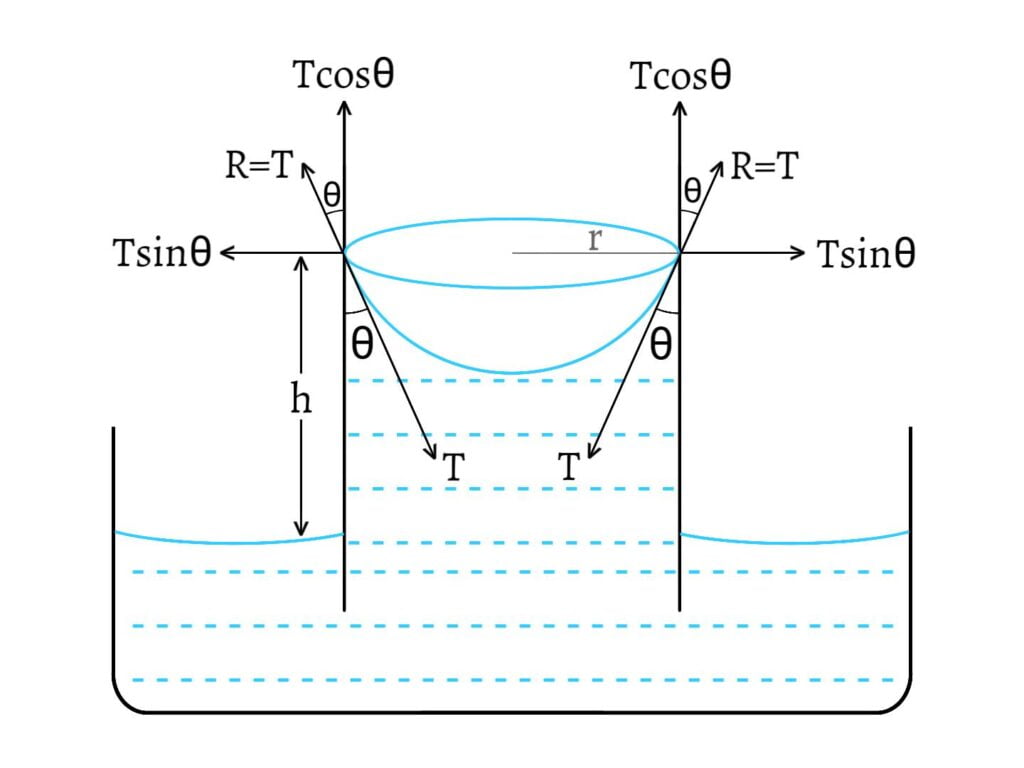
The reaction $R=T$ can be resolved into two components; $T\sin\theta$ and $T\cos\theta$.
$T\sin θ$ acts horizontally and radially outward all along the circle of contact and these components cancel the effects of one another.
$T\cos θ$ acts vertically upward. Thus, total upward force exerted on the liquid, \[=2πrTcosθ\]
Because of these upward force, the liquid rises upto a height $h$ till the weight of the liquid above the free surface becomes just equal to the total upward force. Weight of the liquid above the surface, \[W=mg\] \[W=Vρg\] where, $V$ is the volume of the liquid, $ρ$ is the density of the liquid and $m=Vρ$. \[W=πr^2hρg \text{ [V=πr²h]}\]
In equilibrium state,
Total upward force = Weight of the liquid above the free surface \[\text{i.e.}\;\;2πrT\cos θ=πr^2hρg\] Thus, the value of surface tension is given by, \[T=\frac{rhρg}{2\cos θ}\] The height $h$ to which the liquid rises is given by, \[h=\frac{2T\cos θ}{rρg}\] This expression is known as Ascent formula.
- For the liquid which wets the glass of the tube, angle of contact is acute. So, $\cos θ$ is positive and the liquid rises upward in the tube.
- For the liquid which does not wet the glass of the tube, angle of contact is obtuse. So, $\cos θ$ is negative and the liquid falls downward in the tube.
Rise of Liquid in a Capillary Tube of Insufficient Length
We know that when a capillary tube is dipped into a liquid which wets the glass of the tube, the liquid rises upward in the tube. Now, a question arises –
If a capillary tube of insufficient height is dipped in a liquid, will the liquid overflow?
The answer is no. The liquid does not overflow, it rises upward in the tube by changing the radius of curvature of the meniscus. It is explained briefly below.
Let a tube of radius $r$ be dipped into a liquid of surface tension $T$ and density $\rho$. Then, the liquid rises upto a height $h$ which is given by \[h=\frac{2T\cos\theta}{r\rho g}\;\;\text{__(1)}\] where, $\theta$ is the angle of contact of the liquid.
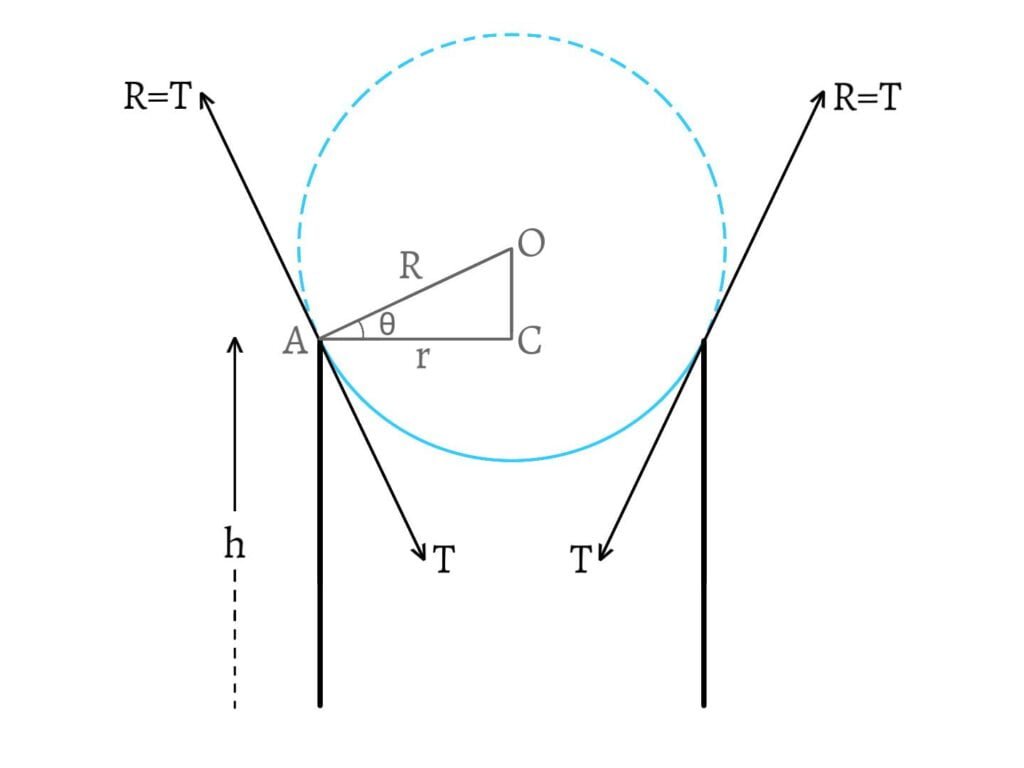
Let $O$ be the centre of curvature of the meniscus and $R$ be its radius. Then, in $\Delta ACO$, \[\cos\theta=\frac{AC}{AO}=\frac{r}{R}\] \[\therefore r=R\cos\theta\;\;\text{__(2)}\]
From $\text{(1)}$ and $\text{(2)}$, \[h=\frac{2T\cos\theta}{R\cos\theta\cdot\rho g}=\frac{2T}{R\rho g}\] \[\therefore hR=\frac{2T}{\rho g}=\text{constant}\]
This relation shows that the radius of curvature of the meniscus depends on the height available for it to expand.
When length of capillary tube is greater than $h$, then $R$ remains constant and height $h$ adjusts itself to satisfy the above relation.
When length of the tube is less than $h$, then $R$ adjusts itself to satisfy the above relation. Less the height, more is the radius of curvature of the meniscus. When $h=0$, $R=\infty$ i.e. the meniscus becomes flat.
Hence, the liquid does not overflow in the capillary tube of insufficient height.
More on Surface Tension
