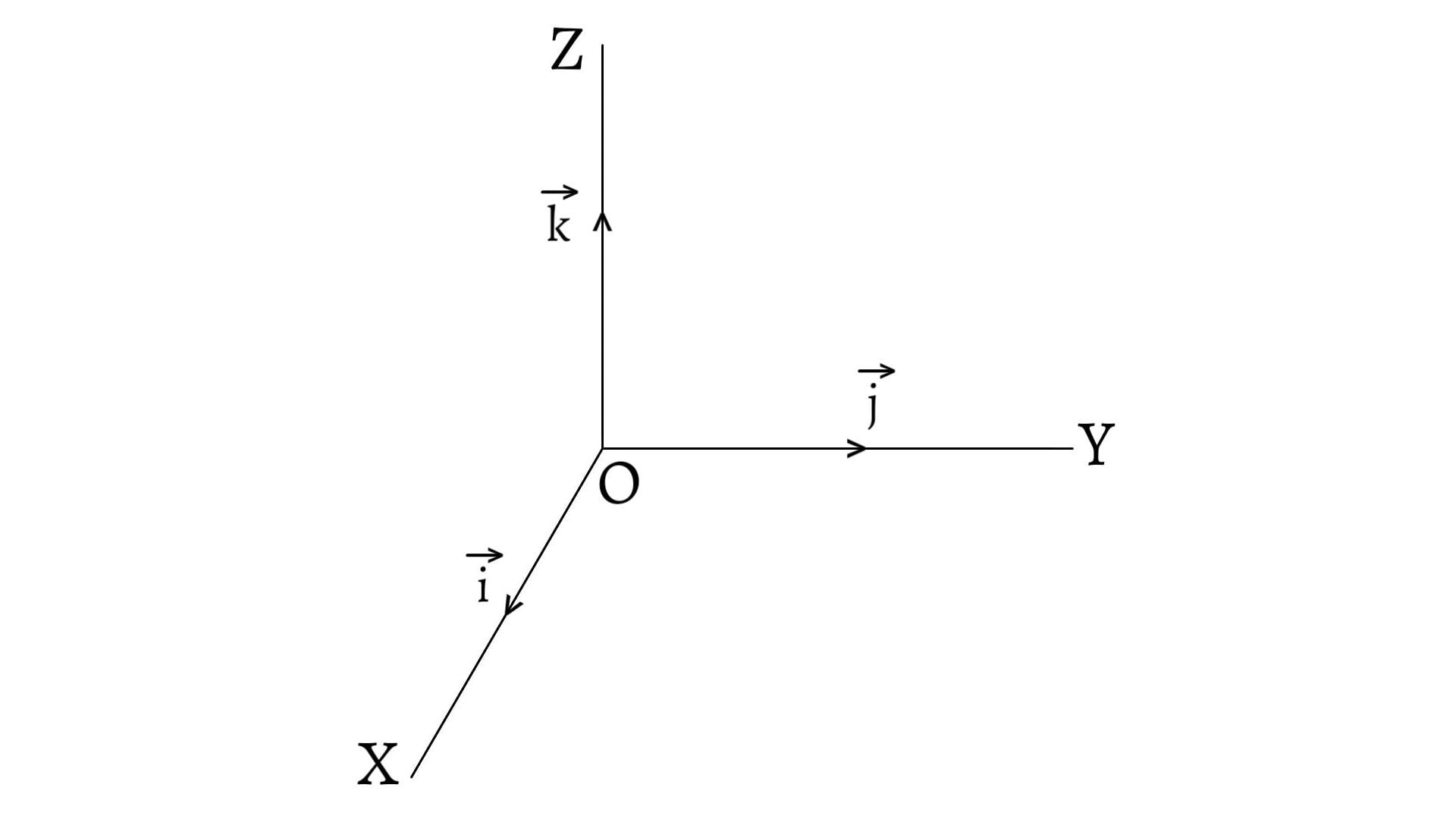
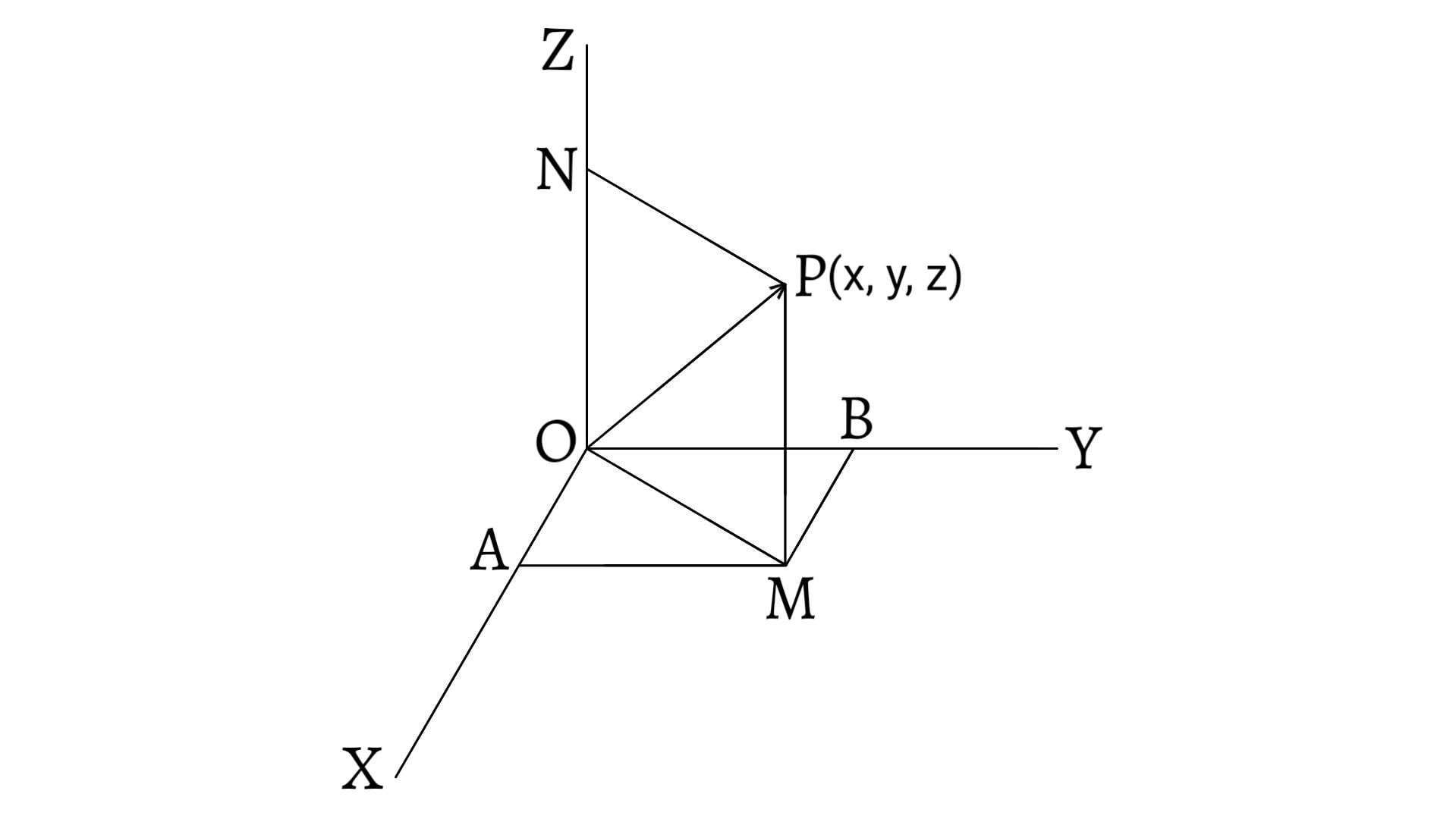
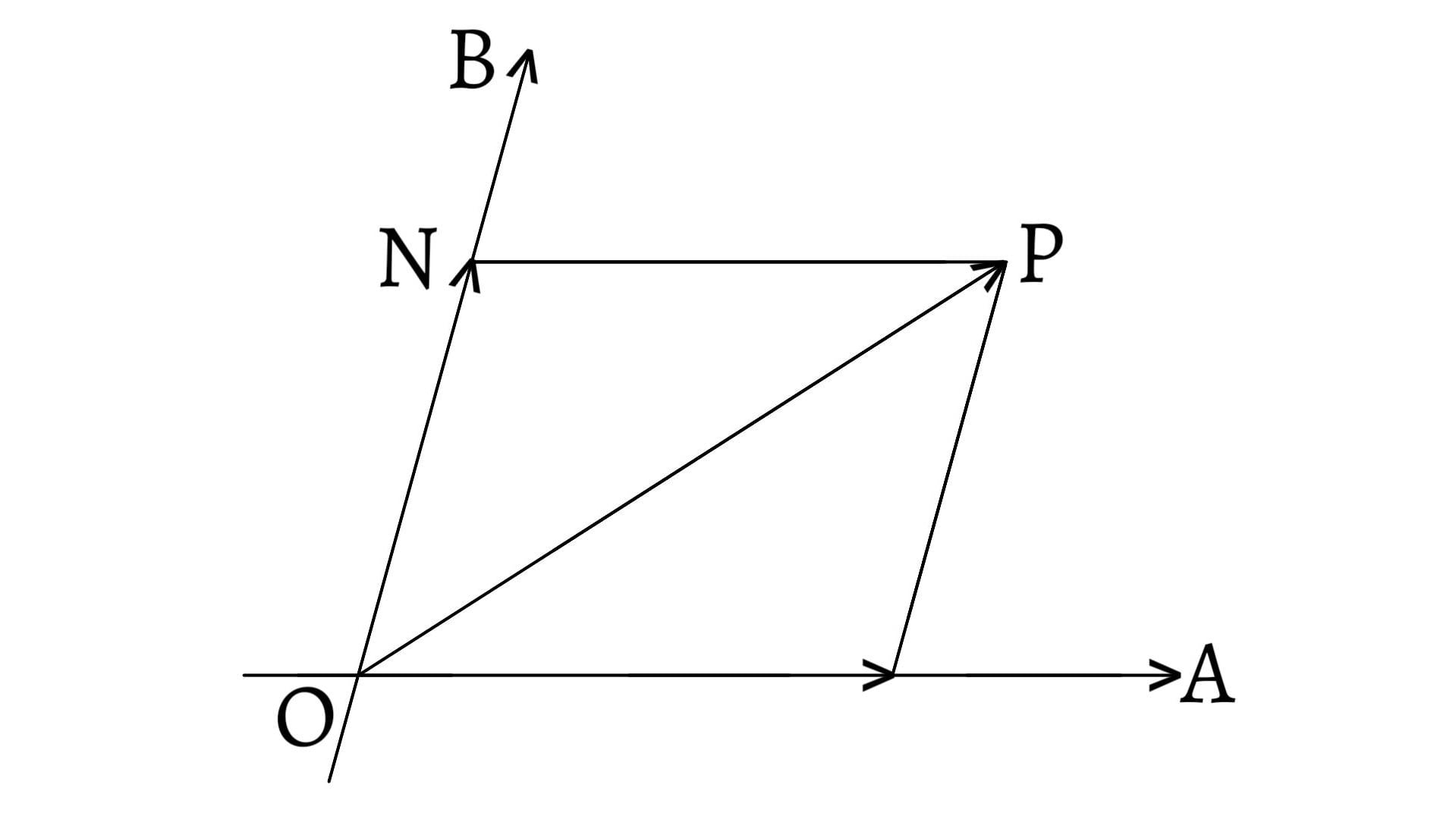
Resolution of a Vector

Resolution of a vector is just opposite to the composition of vectors. It is the process of splitting a single vector into two or more vectors in different directions which together produce the same effect as produced by the single vector alone.

Let a vector $\overrightarrow{R}$ be represented by $\overrightarrow{OB}$. Let $\overrightarrow{P}$ and $\overrightarrow{Q}$ be represented by $\overrightarrow{OA}$ and $\overrightarrow{AB}$.

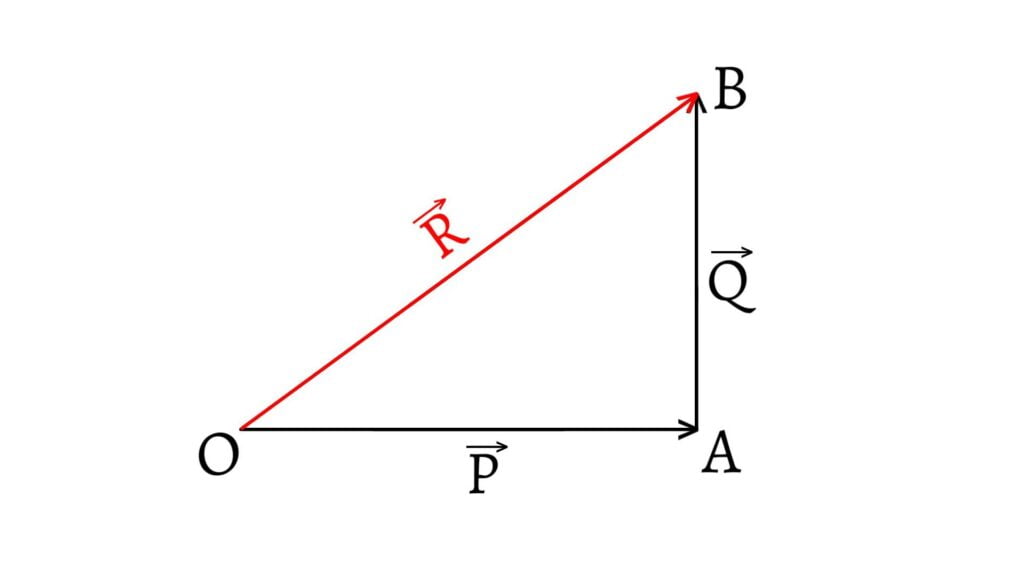
\[\therefore\overrightarrow{OB}=\overrightarrow{OA}+\overrightarrow{AB}\] \[\text{or,}\;\overrightarrow{R}=\overrightarrow{P}+\overrightarrow{Q}\]

Here, the single vector or vector sum $(\overrightarrow{R})$ is also known as the resultant of two vectors. And, the two vectors $(\overrightarrow{P}$ and $\overrightarrow{Q})$ whose sum is a given vector $(\overrightarrow{R})$ are called the components of the given vector.

This process of splitting the resultant vector $(\overrightarrow{R})$ into the components $(\overrightarrow{P}$ and $\overrightarrow{Q})$ is called resolving or resolution of the vector. We often find components parallel to the x-axis and y-axis. Such components are called rectangular components.

Rectangular Components of a Vector in a Plane

When a vector is splitting into two component vectors at right angles to each other, the component vectors are called rectangular components of the vector.

Consider a vector $\overrightarrow{P}$ represented by $\overrightarrow{OC}$, has to be resolved into two rectangular component vectors along the direction of x-axis and y-axis. From the point $O$, draw $OX$ and $OY$ at right angles to represent x-axis and y-axis respectively. From $C$, draw $CA$ and $CB$ perpendiculars to $OX$ and $OY$ respectively.

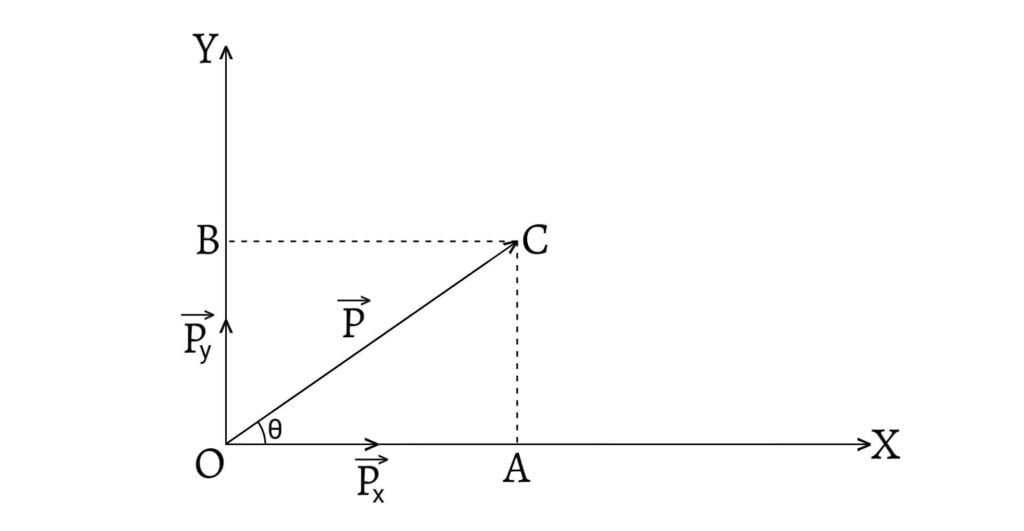
Then, $\overrightarrow{OA}$ $(=\overrightarrow{P_x})$ and $\overrightarrow{OB}$ $(=\overrightarrow{P_y})$ are the rectangular components of $\overrightarrow{P}$. The vector $\overrightarrow{P_x}$ (parallel to x-axis) is called the horizontal component and the vector $\overrightarrow{P_y}$ (parallel to y-axis) is called the vertical component.

Here, $AC$ is equal and parallel to $OB$. Hence, $\overrightarrow{AC}$ also represents $\overrightarrow{P_y}$ in magnitude and direction. From the triangle law of vector addition, in $\Delta OAC$, we have,

\[\overrightarrow{OC}=\overrightarrow{OA}+\overrightarrow{AC}\] \[\therefore\overrightarrow{P}=\overrightarrow{P_x}\:\hat{i}+\overrightarrow{P_y}\:\hat{j}\]

Let the angle between $\overrightarrow{P}$ and $\overrightarrow{P_x}$ be $\theta$, i.e. $\angle AOC=\theta$. In right angled $\Delta AOC$, \[\frac{OA}{OC}=\cos\theta\] \[\therefore OA=OC\cos\theta\] \[\text{or,}\;P_x=P\cos\theta\]

Similarly, \[\frac{AC}{OC}=\sin\theta\] \[\therefore AC=OC\sin\theta\] \[\text{or,}\;P_y=P\sin\theta\] Also, \[OC^2=OA^2+AC^2\] \[P^2=P_x^2+P_y^2\] \[\therefore P=\sqrt{P_x^2+P_y^2}\] and, \[\tan\theta=\frac{AC}{OC}=\frac{P_y}{P_x}\] \[\therefore\theta=\tan^{-1}\left(\frac{P_y}{P_x}\right)\]