Real-valued Functions and Algebra of Real-valued Functions

The functions $ƒ: A\to R$ which associate each element of set $A$ with a unique real number $ƒ(a)$ of set $B$ are called real-valued functions.

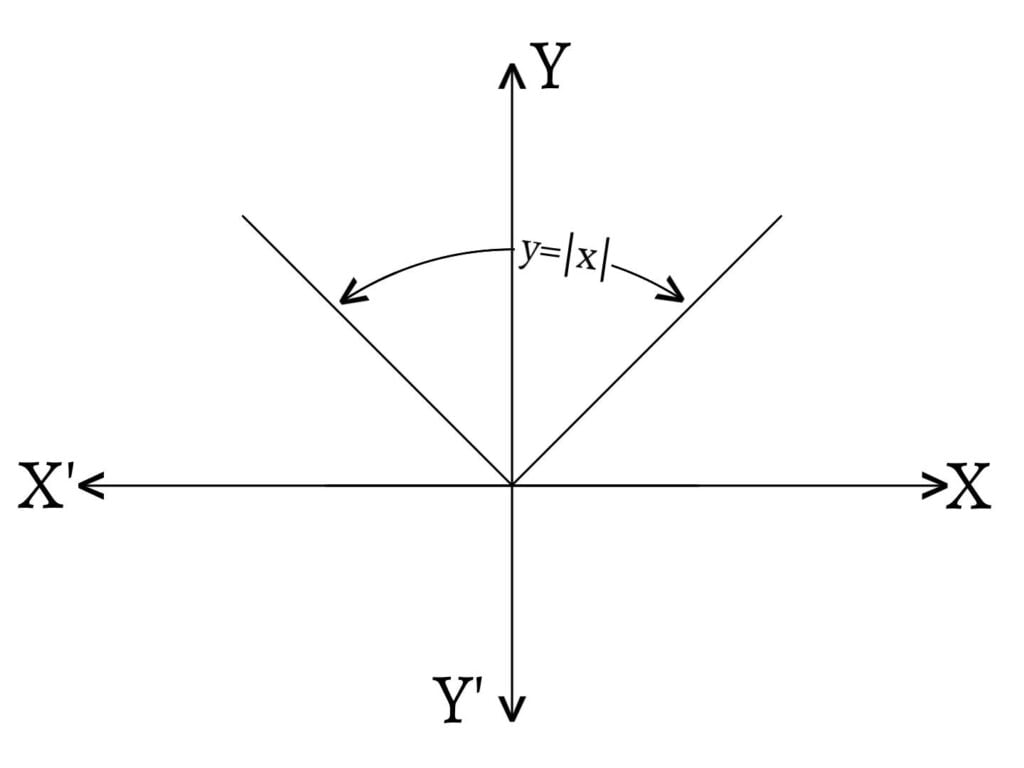
If $x$ is any real number, then the absolute value function defined by \[ƒ(x)=|x|=\left\{\begin{array}{c} x, \text{ if } x≥0 \\ -x, \text{ if } x<0 \end{array}\right.\] is a real-valued function. Its graph is,

Consider two real-valued functions that have the same domain $D$. Suppose $ƒ: D\to R$ and $g: D\to R$ are two real-valued functions and $k$ is a real number. Then, each of the following functions on the left side is defined by the formula on the right: \[(ƒ+k):D\to R \text{ by } (ƒ+k)(x)=ƒ(x)+k\] \[(|ƒ|):D\to R \text{ by } (|ƒ|)(x)=|ƒ(x)|\] \[(ƒ^n):D\to R \text{ by } (ƒ^n)(x)=(ƒ(x))^n\] \[(ƒ±g):D\to R \text{ by } (ƒ±g)(x)=ƒ(x)±g(x)\] \[(kƒ):D\to R \text{ by } (kƒ)(x)=k(ƒ(x))\] \[(ƒg):D\to R \text{ by } (ƒg)(x)=ƒ(x)g(x)\] \[\left(\frac{ƒ}{g}\right):D\to R \text{ by } \left(\frac{ƒ}{g}\right)(x)=\frac{ƒ(x)}{g(x)} \text{ (}g(x)≠0)\] Examples:

Let $ƒ: R\to R$ be defined by $ƒ(x)=x+3$. Then, \[(ƒ+3)(x)=ƒ(x)+3\]\[=(x+3)+3\]\[=x+6\] \[(ƒ^2)(x)=(ƒ(x))^2\] \[=(x+3)^2\] \[=x^2+6x+9\]
Let $ƒ: R\to R$ and $g: R\to R$ be defined by $ƒ(x)=3x-1$ and $g(x)=x^2$. Then, \[(3ƒ-2g)(x)=3ƒ(x)-2g(x)\] \[=3(3x-1)-2x^2\] \[=-2x^2+9x-3\] \[(ƒg)(x)=ƒ(x)g(x)\] \[=(3x-1)x^2\] \[=3x^3-x^2\]

More on Relations And Functions