The boy should row the boat slightly against the flow of water by making some angle with the perpendicular distance joining the two shores.
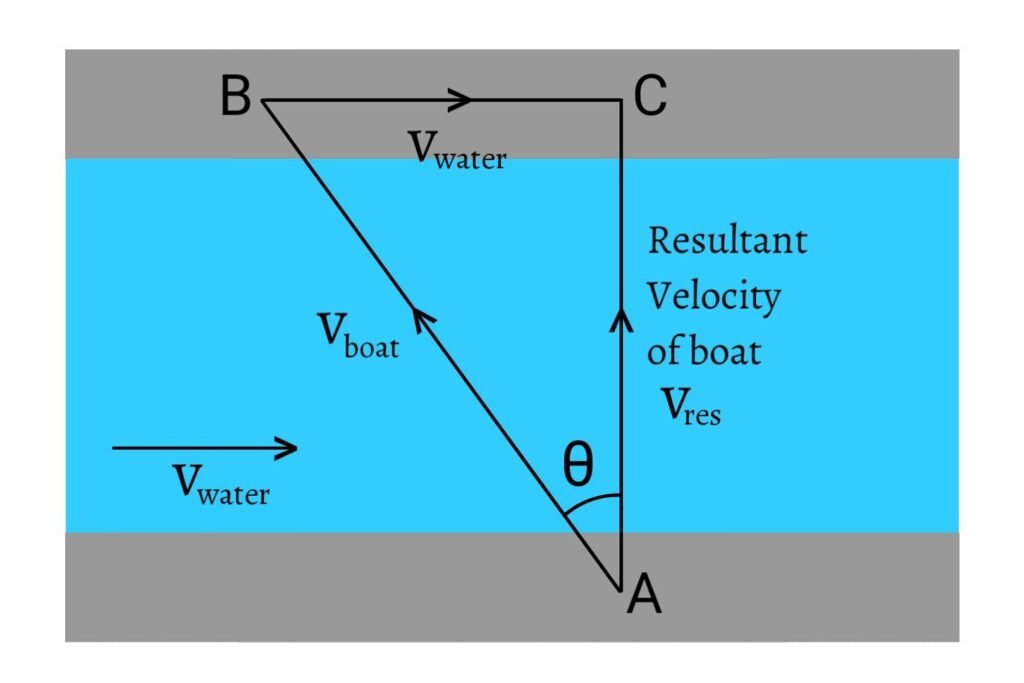
Suppose water is flowing to the right and the boat has to cross from one shore to another as shown in the figure (view from the top). So, he has to row the boat along AB. The resultant of velocity of the water and the boat is along the direction AC. [Triangle Law of Vector Addition]
Let the $v_{\text{boat}}$ and $v_{\text{water}}$ be the velocities of boat and water respectively. Then, the boy should row the boat by making an angle $\theta$ with the perpendicular distance joining the two shores such that
\[\sin\theta=\frac{BC}{AB}=\frac{v_{\text{water}}}{v_{\text{boat}}}\]
\[\therefore\theta=\sin^{-1}\left(\frac{v_{\text{water}}}{v_{\text{boat}}}\right)\]
